高中数学知识点总结_高中数学知识点试题

当前位置：知识点挑题

请展开查看知识点列表

预备知识
函数
几何与代数
概率与统计
数学知识的延伸

更多>>

原创

更新中

【优学堂】2026年高考数学一轮复习

明确考点剖析考向配加典例和变式题真题演练及精选模拟全方位助力备考

浏览次数：3683 更新：2025年06月20日

原创

更新中

《黄金讲练》2025-2026学年人教A版（2019）必修第一册高一同步课堂

知识图解新知探究答疑解惑针对训练

浏览次数：534 更新：2025年06月20日

2211．函数y=6cosx（0＜x＜π）与y=
3
tanx的图象相交于M、N两点，O为坐标原点，则△MON的面积为（　　）
A．2π B．
3
2
π
2
C．
3
π
D．
3
π
2
发布：2024/12/29 0:0:2组卷：406引用：7难度：0.8
解析
2212．动点A（x,y）在圆x²+y²=1上绕坐标原点沿逆时针方向匀速旋转，其初始位置为A₀（
1
2
，
3
2
），12秒旋转一周，则动点A的纵坐标y关于时间t（单位：秒）的函数解析式为（　　）
A．
y
=
sin
（
π
3
t
+
π
6
）
B．
y
=
cos
（
π
6
t
+
π
3
）
C．
y
=
sin
（
π
6
t
+
π
3
）
D．
y
=
cos
（
π
3
t
+
π
6
）
发布：2024/12/29 0:0:2组卷：319引用：3难度：0.5
解析
2213．已知点A（-1，0）和点B关于直线l：x+y-1=0对称．
（1）若直线l₁过点B，且使得点A到直线l₁的距离最大，求直线l₁的方程；
（2）若直线l₂过点A且与直线l交于点C，△ABC的面积为2，求直线l₂的方程．
发布：2024/12/29 0:0:2组卷：502引用：5难度：0.6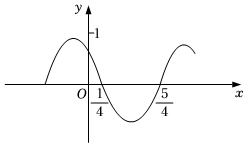
解析
2214．已知函数
f
（
x
）
=
cos
（
ωx
+
φ
）
（
ω
＞
0
，
|
φ
|
＜
π
2
）
的部分图象如图所示，则下列结论正确的是（　　）
A．ω=π
B．
φ
=
π
3
C．
x
=
3
4
是函数的一条对称轴
D．
（
k
+
1
4
，
0
）
（
k
∈
Z
）
是函数的对称中心
发布：2024/12/29 0:0:2组卷：426引用：10难度：0.6
解析
2215．北宋数学家沈括的主要数学成就之一为隙积术，所谓隙积，即“积之有隙”者，如累棋、层坛之类，这种长方台形状的物体垛积，设隙积共n层，上底由a×b个物体组成，以下各层的长、宽依次各增加一个物体，最下层（即下底）由c×d个物体组成，沈括给出求隙积中物体总数的公式为S=
n
6
[（2b+d）a+（b+2d）c]+
n
6
（c-a）．已知由若干个相同小球粘黏组成的几何体垛积的三视图如图所示，则该垛积中所有小球的个数为（　　）
A．83 B．84 C．85 D．86
发布：2024/12/28 23:30:2组卷：88引用：6难度：0.9
解析
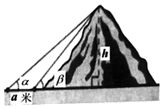2216．某校数学建模社团对校外座山的高度h（单位：m）进行测量，方案如下：如图，社团同学朝山沿直线行进，在前后相距a米两处分别观测山顶的仰角α和β（β＞α），多次测量相关数据取平均值后代入数学模型求解山高，这个社团利用到的数学模型h=
；多次测量取平均值是中学物理测量中常用的减小误差的方法之一，对物理量进行n次测量，其误差ε_n近似满足ε_n～N（0，
2
n
），为使误差ε_n在（-0.5，0.5）的概率不小于0.9973，至少要测量
次．
参考数据：若ξ～N（μ，σ²），则P（μ-3σ＜ξ＜μ+3σ）≈0.9973．
发布：2024/12/28 23:30:2组卷：148引用：5难度：0.6
解析
2217．如图所示，在边长为1的正方形OABC中任取一点P，则点P恰好取自阴影部分（由对角线OB及函数y=x³围成）的概率为
．
发布：2024/12/28 23:30:2组卷：22引用：6难度：0.8
解析
2218．函数y=tanx（-
π
4
≤x≤
π
4
，且x≠0）的值域是

．
发布：2024/12/28 23:30:2组卷：79引用：1难度：0.9
解析
2219．已知
（
2
x
+
1
3
x
）
n
展开式中，第三项的系数与第四项的系数相等．
（1）求n的值；
（2）求展开式中有理项的系数之和（用数字作答）．
发布：2024/12/28 23:30:2组卷：36引用：4难度：0.6
解析
2220．已知正四面体OABC的棱长为2，点G是△OBC的重心，点M是线段AG的中点．
（1）用
OA
，
OB
，
OC
表示
OM
，并求出
|
OM
|
；
（2）求
OM
•
AB
．
发布：2024/12/28 23:30:2组卷：39引用：5难度：0.5
解析

首页上一页 …221 222 223 224 …下一页尾页

A． y = sin （ π 3 t + π 6 ）	B． y = cos （ π 6 t + π 3 ）
C． y = sin （ π 6 t + π 3 ）	D． y = cos （ π 3 t + π 6 ）

2211．函数y=6cosx（0＜x＜π）与y=3tanx的图象相交于M、N两点，O为坐标原点，则△MON的面积为（ ）

2212．动点A（x,y）在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转，其初始位置为A0（12，32），12秒旋转一周，则动点A的纵坐标y关于时间t（单位：秒）的函数解析式为（ ）

2213．已知点A（-1，0）和点B关于直线l：x+y-1=0对称．（1）若直线l1过点B，且使得点A到直线l1的距离最大，求直线l1的方程；（2）若直线l2过点A且与直线l交于点C，△ABC的面积为2，求直线l2的方程．

2214．已知函数f（x）=cos（ωx+φ）（ω＞0，|φ|＜π2）的部分图象如图所示，则下列结论正确的是（ ）

2217．如图所示，在边长为1的正方形OABC中任取一点P，则点P恰好取自阴影部分（由对角线OB及函数y=x3围成）的概率为 ．

2218．函数y=tanx（-π4≤x≤π4，且x≠0）的值域是 ．

2219．已知（2x+13x）n展开式中，第三项的系数与第四项的系数相等．（1）求n的值；（2）求展开式中有理项的系数之和（用数字作答）．

2220．已知正四面体OABC的棱长为2，点G是△OBC的重心，点M是线段AG的中点．（1）用OA，OB，OC表示OM，并求出|OM|；（2）求OM•AB．

2211．函数y=6cosx（0＜x＜π）与y=
3
tanx的图象相交于M、N两点，O为坐标原点，则△MON的面积为（　　）

2212．动点A（x,y）在圆x²+y²=1上绕坐标原点沿逆时针方向匀速旋转，其初始位置为A₀（
1
2
，
3
2
），12秒旋转一周，则动点A的纵坐标y关于时间t（单位：秒）的函数解析式为（　　）

2213．已知点A（-1，0）和点B关于直线l：x+y-1=0对称．
（1）若直线l₁过点B，且使得点A到直线l₁的距离最大，求直线l₁的方程；
（2）若直线l₂过点A且与直线l交于点C，△ABC的面积为2，求直线l₂的方程．

2214．已知函数
f
（
x
）
=
cos
（
ωx
+
φ
）
（
ω
＞
0
，
|
φ
|
＜
π
2
）
的部分图象如图所示，则下列结论正确的是（　　）

2217．如图所示，在边长为1的正方形OABC中任取一点P，则点P恰好取自阴影部分（由对角线OB及函数y=x³围成）的概率为
．

2218．函数y=tanx（-
π
4
≤x≤
π
4
，且x≠0）的值域是

．

2219．已知
（
2
x
+
1
3
x
）
n
展开式中，第三项的系数与第四项的系数相等．
（1）求n的值；
（2）求展开式中有理项的系数之和（用数字作答）．

2220．已知正四面体OABC的棱长为2，点G是△OBC的重心，点M是线段AG的中点．
（1）用
OA
，
OB
，
OC
表示
OM
，并求出
|
OM
|
；
（2）求
OM
•
AB
．