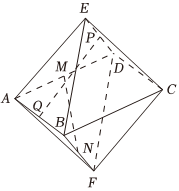
 柏拉图多面体是柏拉图及其追随者对正多面体进行系统研究后而得名的几何体.如图是棱长均为1的柏拉图多面体EABCDF,P,Q,M,N分别为DE,AB,AD,BF的中点,则PQ•MN=( )
柏拉图多面体是柏拉图及其追随者对正多面体进行系统研究后而得名的几何体.如图是棱长均为1的柏拉图多面体EABCDF,P,Q,M,N分别为DE,AB,AD,BF的中点,则PQ•MN=( )
PQ
•
MN
【考点】空间向量的数量积运算.
【答案】A
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/8/25 4:0:8组卷:213引用:13难度:0.7
相似题
-
1.已知
=(3,2,-1),a=(2,1,2).b
(1)求(-a)•(b+2a);b
(2)当(k-a)⊥(b+ka)时,求实数k的值.b发布:2024/12/29 3:0:1组卷:263引用:7难度:0.7 -
 2.如图,在棱长为4的正方体ABCD-A1B1C1D1中,E,F,G分别是A1D1,DD1,CD的中点.以A为坐标原点,的方向为x轴的正方向,建立如图所示的空间直角坐标系.AB
2.如图,在棱长为4的正方体ABCD-A1B1C1D1中,E,F,G分别是A1D1,DD1,CD的中点.以A为坐标原点,的方向为x轴的正方向,建立如图所示的空间直角坐标系.AB
(1)写出B1,C1,E,F,G五点的坐标;
(2)求.C1G•(B1E+B1F)发布:2024/12/29 6:30:1组卷:128引用:7难度:0.8 -
3.已知空间向量
,a=(2,4,-2),b=(-1,0,2).c=(x,2,-1)
(1)若,求a∥c;|c|
(2)若,求b⊥c的值.(a-c)•(2b+c)发布:2024/12/28 23:30:2组卷:81引用:5难度:0.7


