当前位置：
知识点挑题
请展开查看知识点列表
>
<
更多>>
|
原创
更新中
|
解题模型
因材施教
夯实基础
稳步提升
浏览次数：3142
更新：2025年04月25日
|
|
原创
更新中
|
知识图解
新知探究
答疑解惑
针对训练
浏览次数：3445
更新：2025年04月25日
|
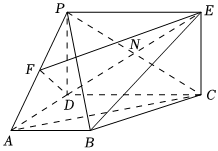181．如图，已知直线PD⊥平面ABCD，四边形ABCD是梯形，四边形PDCE为矩形，线段PC交DE于点N，∠ADC=∠BAD=90°，点F为PA中点，AB=AD=CD=1，PD=12．3
（1）求证：AC∥平面DEF；
（2）求二面角A-BC-P的正弦值；
（3）在线段AP上是否存在一点M，使得BM与平面BCP所成角的正弦值为，若存在，求出线段AM的长；若不存在，请说明理由．3020发布：2025/1/2 8:0:1组卷：30引用：1难度：0.6182．过正三棱柱底面一边的截面是（ ）
发布：2025/1/2 8:0:1组卷：83引用：3难度：0.9183．水平放置的平面四边形ABCD的斜二测直观图为一个上底为1，下底为2，高为10的梯形，则四边形ABCD的实际面积为（ ）
发布：2025/1/2 8:0:1组卷：44引用：1难度：0.8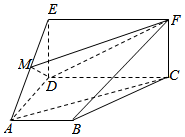
184．如图，四边形ABCD是梯形．四边形CDEF是矩形．且平面ABCD⊥平面CDEF，∠BAD=90°，AB∥CD，M是线段AE上的动点．
（Ⅰ）试确定点M的位置，使AC∥平面DMF，并说明理由；
（Ⅱ）在（Ⅰ）的条件下，且∠AED=45°，AE=，AD=2CD，连接AF，求三棱锥M-ADF的体积．12发布：2025/1/2 8:0:1组卷：29引用：1难度：0.3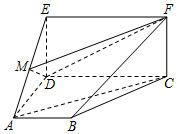
185．如图，四边形ABCD是梯形，四边形CDEF是矩形，且平面ABCD⊥平面CDEF，∠BAD=∠CDA=90°，AB=AD=DE=CD=2，M是AE的中点．12
（1）证明：AC∥平面MDF；
（2）求平面DMF与平面ABCD所成锐二面角的余弦值．发布：2025/1/2 8:0:1组卷：62引用：1难度：0.6
186．如图，四边形ABCD是梯形．四边形CDEF是矩形．且平面ABCD⊥平面CDEF，∠BAD=90°，AB∥CD，AB=AD=DE=CD，M是线段AE上的动点．12
（Ⅰ）试确定点M的位置，使AC∥平面DMF，并说明理由；
（Ⅱ）在（Ⅰ）的条件下，求平面DMF与平面ABCD所成锐二面角的余弦值．发布：2025/1/2 8:0:1组卷：40引用：3难度：0.3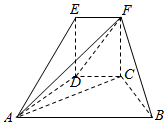
187．如图所示多面体ABCDEF中，四边形ABCD是一个等腰梯形，四边形CDEF是一个矩形，AB∥CD，AC⊥FB，∠ABC=60°，BC=CD=2，CF=3．
（1）求证：FC⊥面ABCD；
（2）求三棱锥E-ADF的体积．发布：2025/1/2 8:0:1组卷：57引用：1难度：0.6188．给出下列图形：①角；②三角形；③平行四边形；④梯形；⑤四边形．其中表示平面图形的个数为（ ）
发布：2025/1/2 8:0:1组卷：122引用：2难度：0.9189．将序号分别为1，2，3，4，5的5张参观券全部分给4人，每人至少1张．如果分给同一人的2张参观券连号，那么不同的分法种数是（ ）
发布：2025/1/2 7:0:3组卷：216引用：5难度：0.7190．已知ab＞0，bc＜0，则直线ax+by+c=0通过（ ）
发布：2025/1/2 2:30:3组卷：576引用：8难度：0.9
